| I-
DÉFINITIONS RELATIVES A LA PARENTE
II- ILLUSTRATIONS
III- EFFET DU
CHOIX DU CONJOINT SUR LA STRUCTURE DU PATRIMOINE GÉNÉTIQUE
D'UNE POPULATION
IV- CONSÉQUENCE
EN MATIÈRE DE SANTÉ PUBLIQUE
I- DÉFINITIONS
RELATIVES A LA PARENTE:
1°- La consanguinité:
soit le couple K et L, il s'agit d'un
mariage entre apparentés
I , leur enfant est consanguin
K et L peuvent chacun avoir reçu
de leur ancêtre commun A, la copie d'un même gène, parmi
les 2 que possédait l'ancêtre.
Les deux copies identiques, appelés
gènes identiques par ascendance, peuvent alors être transmises
à l'enfant consanguin qui sera, de ce fait, homozygote = autozygote.
Il est également clair et évident
qu'un enfant consanguin sera en moyenne (sur un grand nombre de loci)
plus homozygote qu'un enfant issu d'une union entre individus non apparentés.
2°- Gènes identiques
par ascendance:
On dit que deux gènes sont identiques
par ascendance quand ils ont la copie d'un même gène ancêtre.
Si on néglige l'effet des mutations,
ces gènes identiques par ascendance sont évidemment porteurs
de la même information génétique : ce sont 2 allèles
identiques.
3°- coefficient de
parenté:
On appelle 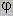 KL, coefficient de parenté de deux individus K et L, la probabilité
qu'un gène pris au hasard, à un locus quelconque de
K, soit identique par descendance à un gène, pris au hasard,
au même locus chez L.
KL, coefficient de parenté de deux individus K et L, la probabilité
qu'un gène pris au hasard, à un locus quelconque de
K, soit identique par descendance à un gène, pris au hasard,
au même locus chez L.
Il s'agit d'une mesure de la parenté
entre K et L. On doit se contenter seulement de 2 ou 3 générations
parce qu'après la parenté devient négligeable.
4- Coefficient de consanguinité
:
On appelle FI, coefficient
de consanguinité de l'individu I, la probabilité que, à
un locus quelconque de I, les deux gènes homologues présents
soient identiques par ascendance. L'individu I est alors homozygote.
Cette définition s'applique aux
gènes autosomaux et aux gènes liés à l'X, chez
les individus de sexe féminin.
5°- Relation
entre les coefficients de parenté 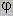 KL
et de consanguinité FI KL
et de consanguinité FI
Les deux définitions ont été
calculées de sorte que le 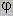 KL
est égal au FI: c'est le coefficient de Malecot (1948). KL
est égal au FI: c'est le coefficient de Malecot (1948).
En effet, comparer l'identité par
ascendance des 2 gènes d'un individu consanguin (définition
du coefficient de consanguinité F) revient au même que de
comparer deux gènes pris au hasard, chez chacun des
parents (coefficient de parenté 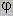 ) )
FI = 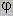 KL KL
6- Formule mathématique
du 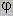 ou F: ou F:
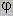 KL
pour que deux gènes, tirés au même locus, l'un chez
K, l'autre chez L, soient identiques par ascendance, il faut réunir
simultanément deux conditions ou événements KL
pour que deux gènes, tirés au même locus, l'un chez
K, l'autre chez L, soient identiques par ascendance, il faut réunir
simultanément deux conditions ou événements
- 1er événement : les 2
gènes doivent venir du même ancêtre commun (c'est l'identité
de provenance)
- 2ème événement:
les deux gènes doivent être tous les 2 une copie du même
gène ancestral (identité de copie sachant l'identité
de provenance).
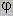 KL
sera le produit des probabilités de ces 2 événements. KL
sera le produit des probabilités de ces 2 événements.
La probabilité du 1er événement
est égale à:
(1/2)i X (1/2) j = (1/2) (i+j)
i = le nombre de générations
allant de K à A
j = le nombre de générations
allant de L à A
puisque, à chaque fois, en remontant
de K à A ou de L à A, la probabilité déprendre
un gène venant d'un descendant de A est égale à 1/2,
et cela i ou j fois de suite.
La probabilité du 2ème événement
puisque A présente pour chaque
gène 2 allèles; la probabilité qu'il donne le
même gène à K et à L est de 1/2.
Si les 2 allèles (gènes)
présents chez A sont eux mêmes identiques par ascendance (A
est lui même consanguin), l’événement de probabilité
est égale à FA (par définition).
1/2 + (1/2) fA : c'est la probabilité
d'identité de copie sachant l’identité de provenance, La
probabilité 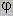 KL
recherchée est donc le produit des probabilités qui
viennent d'être calculées, soit KL
recherchée est donc le produit des probabilités qui
viennent d'être calculées, soit
Identité de copie (A est consanguin)
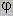 KL
= (1/2)(i+j) x [(1/2) + (1/2 FA)] KL
= (1/2)(i+j) x [(1/2) + (1/2 FA)]
(1/2)(i+j)=Identité
de provenance
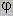 KL
= (1/2)(i+j+1) dans le cas d'un ancêtre
commun, non consanguin ou dont la consanguinité est inconnue (FA
= O : Coefficient de consanguinité de l'ancêtre) KL
= (1/2)(i+j+1) dans le cas d'un ancêtre
commun, non consanguin ou dont la consanguinité est inconnue (FA
= O : Coefficient de consanguinité de l'ancêtre)
II- ILLUSTRATIONS:
A/ Calcul du coefficient de parenté
entre 2 cousins demi-germains K et L, ayant un seul ancêtre commun
A.
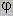 KL
= (1/2) (i+j+1) KL
= (1/2) (i+j+1)
Probabilité que l'un ou l'autre
des allèles de l'ancêtre commun A ait été transmis
à K par AMK = (1/2)2
à L par APL = (1/2)2
donc probabilité (1/2) 2+2+1
= 1/32.
(FA = O)
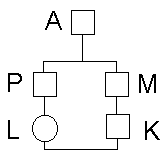
B/ Calcul du coefficient de consanguinité
d'un enfant né d'un mariage entre cousins germains (2 ancêtres
communs).
Pour un locus donné A présente
2 alléles · et o.
Probabilité que l'allèle
· ait été transmis
à I par la voie AMKI = (l/2)3
= 1/8
à I par la voie APLI = (112)3
= 1/8
- La probabilité que I possède
2 allèles identiques par ascendance venant de A est (1/8)2
= 1/64
Même raisonnement pour l'autre allèle
o de A probabilité que les 2 allèles A soient identiques
par ascendance = 1/64
La probabilité que les deux gènes
de I soient identiques et issus de A est donc 1/64+1/64 = 1/32 soit
··
soit
oo.
Par raisonnement analogue, la probabilité
que les deux gènes de I soient identiques par ascendance mais issus
de B est aussi 1/32.
Par conséquent, la probabilité
que les deux gènes de I soient identiques par ascendance, issus
de l'un ou de l'autre des deux ancêtres A et B, est 1/32+ 1/32 =
1/16 = FI.
C'est le coefficient de consanguinité
de l'enfant I né d'un mariage entre cousins germains de 1er degré
(1/16 du génotype est homozygote).

III- EFFET
DU CHOIX DU CONJOINT SUR LA STRUCTURE DU PATRIMOINE GENETIQUE D'UNE POPULATION:
Dans une population humaine,
seule une partie des unions sont panmictiques.
Les autres obéissent à des règles de choix du conjoint,
dictées par des traditions locales, culturelles, religieuses ou
socio-économiques.
Dans ces conditions on peut définir
un coefficient moyen de parenté comme la moyenne des
coefficients de parenté des conjoints
d'une génération donnée (on supposera que les générations
sont séparées).
Quel sera l'effet de ce choix du conjoint
sur le patrimoine génétique, quand on suppose valides
les autres conditions de l'équilibre de Hardy-Weinberg?
Prenons l'exemple d'un Cas simple d'un
gène avec 2 allèles : A, de fréquence p, et a de fréquence
q, chez les parents
- les deux allèles sont identiques
par ascendance, avec une probabilité égale à FI
.Les deux allèles ne peuvent jamais être différents,
et la probabilité d'avoir A et a est donc égale à
0.
- les deux allèles peuvent
ne pas être identiques par ascendance
(conditions Hardy-Weinberg) : la probabilité
est égale à 1-FI.
Conditions Hardy-Weinberg
La probabilité d'un génotype
A/A donnant un phénotype A = p2.
La probabilité d'un génotype
a/a donnant un phénotype a = q2.
La probabilité d'un génotype
A/a ou a/A donnant un phénotype A,a = 2pq
Dans une population générale
où une partie est panmictique et l'autre est consanguine:
|
|
alléles
identiques par ascendance
(consanguinté) |
alléles non identiques
par ascendance
(panmixie) |
| A/A |
F(A/A) |
FI x p |
(1-FI) x p2 |
| A/a |
F(A/a) |
FI x 0 |
(1-FI) x 2pq |
| a/a |
F(a/a) |
FI x q |
(1-FI) x q2 |
Ces fréquences peuvent être
simplifiées et s'écrire
f(A/A) = p2
+ FI.p.(1-p)
f(A/a) = 2pq - 2.FI.pq
f(a/a) = q2
+ FI.q.(i-q)
Exemple
La phényl-cetonurie
Génotype aa = absence de l'enzyme
phenyl-hydroxylase
Fréquence q de l'allèle
a : 1.10-2
Fréquence q2
du génotype a/a = 10-4
Pour un enfant I né de parents
cousins-germains : FI = 1/16
f(a/a) = q2 + FI q (1-q) =
q2+ 1/16 pq = 7.10-4,
valeur 7 fois supérieure à celle trouvée dans une
population panmictique
Ces résultats conduisent à
quelques conclusions
1 - Les fréquences alléliques
dans une grande population ne sont pas modifiées par le choix du
conjoint en fonction de la parenté
2- Les fréquences génotypiques
sont modifiées et ne sont plus celles d e Hardy-Weinberg
3 - Ces fréquences génotypiques,
dites de Wright, sont changées à chaque génération
(i+1) en fonction de la parenté moyenne FI réalisée
chez les conjoints de la génération précédente
i.
IV- CONSEQUENCE
EN MATIERE DE SANTE PUBLIQUE:
Pathologie récessive et pathologie
dominante: la pathologie d'origine génétique dans une population
correspond, en simplifiant à la somme des fréquences des
phénotypes atteints. c'est à dire s'il y a panmixie:
-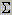 d
(pd2 + 2pdq),
pour l'ensemble des maladies dominantes, où pd
est la fréquence de la mutation morbide dominante de la maladie
d. d
(pd2 + 2pdq),
pour l'ensemble des maladies dominantes, où pd
est la fréquence de la mutation morbide dominante de la maladie
d.
- 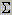 r(qr2),
pour l’ensemble des maladies récessives,
où qr est la fréquence de
la mutation morbide récessive de la maladie r r(qr2),
pour l’ensemble des maladies récessives,
où qr est la fréquence de
la mutation morbide récessive de la maladie r
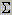 d
(pd2 + 2pdq)
+ d
(pd2 + 2pdq)
+ 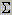 r (qr2)
pour l'ensemble des maladies dominantes et récessives. r (qr2)
pour l'ensemble des maladies dominantes et récessives.
Le poids, en santé publique, de
la pathologie d'origine génétique dérive directement
du polymorphisme de son patrimoine génétique
et de l'importance des fréquences des allèles morbides
qu'il renferme.
Le choix du conjoint en fonction de la
parenté (consanguinité) va augmenter la fréquence
des génotypes homozygotes, et va donc augmenter la fréquence
des maladies génétiques récessives. L'accroissement
relatif de la fréquence de la maladie est égal
à l'accroissement absolu sous un régime non panmictique F.q.(1-q)
rapporté à la fréquence de la maladie sous le régime
panmictique q2, soit F.q (1-q)/q2
= F/q, car la valeur de q est presque toujours très faible.
Cet accroissement relatif (la multiplication
des cas due au choix du conjoint) sera d'autant plus grand que la
consanguinité (ou la parenté moyenne des parents) est
élevée et que la maladie est rare (fréquence q très
faible).
Ce qui illustre le triple exemple
CF ou FKP (Fibrose kystique du pancréas
ou cystic fîbrosis)
PCU (Phényl cétonurie)
GaI (Galactosémie)
dans une population où le taux
moyen de consanguinité est de 1/100.
| Maladie |
fréquence q de l'alléle
morbide |
q2 équilibre de HW |
fréqence Wright
q2+Fq(1-q)
accroissement absolu |
accroissement relatif
F/q
(%) |
| CF ou FKP |
1/50 |
1/2500 |
1/2500+1/5000 |
50 |
| PCU |
1/100 |
1/10.000 |
1/10.000+1/10.000 |
100 |
| Gal |
1/200 |
1/40.000 |
1/40.000+1/20.000 |
200 |
Pour une maladie exceptionnelle,
elle devient rare lorsqu'il y a consanguinité. L'augmentation de
la fréquence de l'accroissement est fonction de la fréquence
q.
 
|



